L’uso dei metodi interferenziali per misura di piccoli spessori è molto interessante, anche per gli studenti, ma richiede apparati interferometrici difficilmente a disposizione di un istituto scolastico.
Anche per questo è interessante l’esperienza che viene di seguito proposta, resa possibile dalla collaborazione con l’Istituto Nazionale di Ottica del C.N.R. di Firenze, che ha messo a disposizione del docente la strumentazione necessaria.
Da un dialogo con un gruppetto di miei alunni della classe V E1, è nata l’idea di approfondire un argomento centrale e significativo della fisica liceale. La scelta è caduta sui fenomeni luminosi, traendo spunto dal titolo del convegno ScienzaAfirenze del 2015, La luce come mezzo di studio e oggetto di indagine, a cui per vari motivi quest’anno, pur desiderandolo, non abbiamo potuto partecipare.
Senza dubbio, la luce è uno degli enti fisici più sorprendenti e belli da studiare, e il fisico Vasco Ronchi lo evidenzia bene : «La luce è per il mondo qualche cosa di basilare, qualche cosa di vitale, che caratterizza il principio della vita e dell’ordine, in contrapposizione alle tenebre del caos, del disordine, della morte. Senza la luce, la terra era inanis et vacua» [b].
Tra tutti i fenomeni luminosi abbiamo scelto di studiare sperimentalmente un’applicazione dell’interferenza.
Richiami sull’interferenza
Come è noto, Thomas Young (1773-1829) riuscì per primo, con il celebre esperimento della doppia fenditura, a mettere in evidenza che la luce manifesta una natura ondulatoria: ovvero, si ha interferenza proprio come per le onde che si propagano in un mezzo elastico.
Rivediamo brevemente alcune proprietà delle onde meccaniche e dell’interferenza tra onde meccaniche. In particolare un’onda armonica è moto armonico che si propaga senza spostamento di materia; l’interferenza tra due onde viene descritta da una funzione d’onda che si ottiene sommando gli spostamenti di due o più onde generate separatamente.
Come esempio, calcoliamo la risultante di due onde armoniche trasversali di uguale frequenza e ampiezza a, che si propagano nella stessa direzione, quella positiva di un sistema di riferimento a coordinata x, lungo una molla di costante elastica k, generate da due sorgenti in fase tra loro, ma con una differenza Δx di cammino percorso.
Inoltre, gli spostamenti lungo un y perpendicolare all’asse delle x sono dati da:

Lo spostamento risultante è: y=y1+y2 e usando le formule di prostaferesi si ha che:
![]() Ricordiamo che all’onda è associata un’energia, somma di energia cinetica e potenziale e che l’energia meccanica E di un punto del mezzo elastico, che oscilla senza attrito, rimane costante, e coincide con l’energia potenziale massima, per cui:
Ricordiamo che all’onda è associata un’energia, somma di energia cinetica e potenziale e che l’energia meccanica E di un punto del mezzo elastico, che oscilla senza attrito, rimane costante, e coincide con l’energia potenziale massima, per cui:
E = K(energia cinetica) +U(energia potenziale elastica) = Umax =
![]() Questa relazione mostra che l’energia E è direttamente proporzionale al quadrato dell’ampiezza
Questa relazione mostra che l’energia E è direttamente proporzionale al quadrato dell’ampiezza ![]() per il fattore d’interferenza.
per il fattore d’interferenza.
Studiamo l’andamento dell’energia in funzione della differenza di fase k Δx.
L’energia è nulla per un certo insieme di valori di Δx,, che corrispondono all’annullarsi della funzione coseno, quando cioè:
![]()
L’energia si annulla anche per:
![]()
E così via si possono trovare tutti i punti in cui E = 0.
Il grafico di ![]() in funzione di k Δx è riportato nella figura che segue:
in funzione di k Δx è riportato nella figura che segue:

Il grafico mostra un alternarsi di massimi e minimi al variare della differenza di fase; come si vede 4 è il valore massimo, 0 è il valore minimo. Calcolando con un integrale il valor medio della funzione si trova infine come valore medio della funzione 2.
Per la luce accade qualcosa di molto simile. Anche la luce ha una natura ondulatoria, e trasporta un’energia, anche se di tipo non meccanico, ma elettromagnetico. Infatti, se consideriamo due fasci luminosi generati da due sorgenti mutuamente coerenti e andiamo a osservare su uno schermo l’effetto dell’azione simultanea dei due fasci, notiamo zone di massima luminosità che si alternano a zone di minima luminosità.
Questa redistribuzione dell’energia è tipica di due onde che interferiscono, come si vede nella figura precedente. Tali zone luminose che si alternano alle zone buie, visibili sullo schermo, sono dette frange di interferenza.
L’apparato sperimentale
Per iniziare a lavorare con l’interferenza della luce ci siamo rivolti al dottor Vincenzo Greco, ricercatore presso l’Istituto Nazionale di Ottica del C.N.R. di Firenze. Il suo gruppo ci ha fornito la strumentazione necessaria e gli ambienti adeguati per effettuare le nostre indagini.
Abbiamo utilizzato tecniche interferometriche per determinare sperimentalmente la curva caratteristica, differenza di potenziale–allungamento, di una particolare ceramica piezoelettrica.
Ricordiamo che con il termine piezoelettricità si intende la proprietà di certi cristalli di generare una carica elettrica se sottoposti a carico meccanico dovuto a pressione o tensione. Tale processo è chiamato effetto piezoelettrico diretto. Viceversa, se sottoposti a un campo elettrico questi cristalli subiscono una deformazione controllata, fenomeno definito effetto piezoelettrico inverso.
Noi abbiamo utilizzato questo effetto. L’interferometro da noi utilizzato è del tipo Twyman-Green (una variante del celebre interferometro di Michelson-Morley). Per migliorare le condizioni sperimentali ci siamo recati nella stanza dei collaudi ottici che è isolata termicamente (20 °C), con aria depurata (senza polveri) da dei filtri e con tavolo anti-vibrazioni per limitare l’errore sulle misure. All’ingresso del laboratorio abbiamo indossato una tuta e un copricapo per limitare l’immissione di polveri o sostanze inquinanti nell’ambiente, in modo da farlo rimanere inalterato.
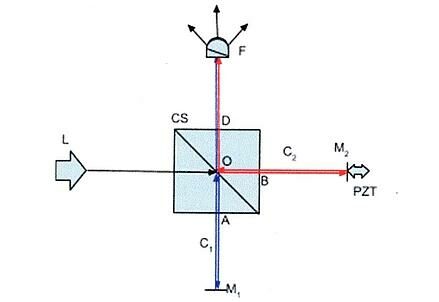
Il nostro interferometro (schematizzato nella figura che segue) è composto da quattro piedistalli (L, M1, M2 e F) su cui sono montati rispettivamente: una sorgente laser, uno specchio fisso, uno specchio mobile collegato alla ceramica piezoelettrica e un obiettivo di microscopio.

L’elemento centrale dell’apparato sperimentale è il cubo semiriflettente (CS) con indice di rifrazione n. Il cubo e gli specchi sono posti in maniera che i fasci laser si riflettano sugli specchi e attraversino CS ortogonalmente.
Il laser L emette un fascio di luce rossa di lunghezza d’onda λ=632.8 nm e di frequenza f = 4,71014 Hz che incontra CS e prosegue fino a raggiungere O, il centro del cubo; qui si divide in due fasci laser, C1 (blu) e C2 (rosso).
In C1 la luce raggiunge lo specchio M1 passando per il punto A, qui viene riflesso e torna indietro, passando per A, O e D fino ad arrivare in F.
La luce passante per C2, invece, arriva fino a M2, fissato sulla ceramica piezoelettrica PZT, passando per B, viene riflesso e arriva in F passando per B, O e D.
In F il raggio passa attraverso un obiettivo di microscopio, necessario per ingrandire il fascio di luce. Ricomponendo i due raggi, a causa della differenza di cammino, si producono delle frange di interferenza che sono proiettate su di un foglio fissato alla parete del laboratorio.
Nella figura seguente è riportata la fotografia dell’apparato sperimentale utilizzato.

La taratura di una ceramica piezoelettrica.
Una volta posizionato l’interferometro osserviamo sulla parete un insieme di frange rosse verticali, (figura che segue), e allineiamo le frange con un segno da noi tracciato sul muro, parallelo alle strisce che rappresenta il nostro zero.

Per allineare la frangia centrale con lo zero abbiamo usato un potenziometro con regolazione micrometrica collegato alla ceramica piezoelettrica e alla sorgente di differenza di potenziale (ddp).
Variando la tensione con il potenziometro, il cristallo piezoelettrico si deforma, muovendo lo specchio a cui è attaccato. (si veda lo schema che segue)

Questo movimento dello specchio M2 determina a sua volta lo spostamento delle frange. Infatti, abbiamo osservato uno spostamento verso destra delle frange rispetto al segno tracciato.
Questo ci ha permesso di effettuare misure con le quali abbiamo compilato una tabella che mette in relazione il numero di frange che attraversano lo zero con la tensione ai capi della ceramica.
Dai dati sperimentali proviamo a costruire un modello lineare per il grafico ddp-Δx relativo all’intervallo da noi misurato (si veda la figura precedente). Possiamo vedere che l’allungamento Δx della ceramica dipende linearmente dalla ddp ai capi della ceramica.
Ogni frangia corrisponde a uno spostamento di λ/2⋍316.4 nm: è così possibile determinare sperimentalmente l’allungamento della sostanza piezoelettrica.
È stato quindi possibile fare una regressione lineare per mettere in relazione i vari punti raccolti con le misurazioni, e abbiamo trovato che la proporzionalità diretta tra ddp e Δx esiste ed è verificata con ottima approssimazione dato che r2 è molto vicino a 1 (0.996).
|
y = 27.4x – 2504.8
|
Conclusioni
Grazie all’interferometro di Twyman-Green da noi usato nell’esperimento siamo riusciti a misurare con buona precisione le caratteristiche di una particolare ceramica piezoelettrica in un dato intervallo di tensione (da 90 a 200 V). Abbiamo verificato che l’allungamento della ceramica è direttamente proporzionale alla tensione ai capi della ceramica, infatti r2 è vicino a 1 e ciò significa che tutti i punti raccolti sono molto vicini alla retta di regressione:
y = 27.4x – 2504.8
Gli errori commessi sono stati ridotti al minimo grazie all’ambiente e agli strumenti con cui sono state fatte le misurazioni; infatti l’errore più grande è stato quello di sensibilità sulla misura della distanza delle frange, apprezzabile solo fino λ/8, circa 79 nm su ogni misurazione; tutti gli altri errori sono trascurabili.
Michele Donvito
(Docente di Matematica e Fisica al Liceo Scientifico “A. Gramsci” di Firenze)
Nota
-
Gli studenti della V E del Liceo scientifico “A. Gramsci”di Firenze che hanno realizzato questa attività sperimentale, nell’anno scolastico 2014 – 2015, sono: Guri Amhed, Filippo Sciammacca e Tiziano Bacci che ha approfondito in particolare la struttura teorica della misura.
Indicazioni bibliografiche
-
E. A. Jenkins, H. E. White, Ottica, Istituto Editoriale Universitario, Milano 1972.
-
Vasco Ronchi, La storia della luce, Laterza Bari 1983.
-
P. Marazzini, M.E. Bergamaschini, L. Mazzoni, Fenomeni, Leggi, Esperimenti, Vol. D, Minerva Scuola, Milano 2012.
© Pubblicato sul n° 59 di Emmeciquadro